Stream Ciphers

  

Stream ciphers are symmetric-key ciphers (i.e., encryption and decryption use the same key) that perform bit-by-bit encryption. In a stream cipher, any bit of the ciphertext depends on a single bit of the plaintext (and the encryption key). Stream ciphers differ from the other big class of symmetric ciphers - the block ciphers, which encrypt block-by-block. In a block cipher, the bits in a ciphertext block depend on (ideally) all bits in the corresponding plaintext block. To the extreme, a stream cipher is a particular type of block cipher with the block's length equal to 1. Compared to block ciphers, stream ciphers are usually faster, but the test of time shows them less secure in general.

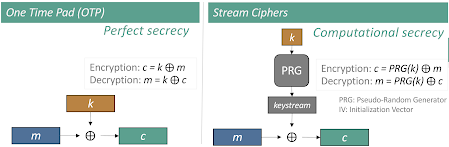
A stream cipher can be seen as the analog of the One Time Pad (OTP) (see Perfect Secrecy and the One Time Pad (OTP)) in computational security. Recall OTP, for which encryption is simply a bitwise XOR between the plaintext and the encryption key. The same holds for the stream ciphers, with the difference that the cryptographic keystream used to encrypt (and thus, decrypt) is not random, but it is the output of a secure Pseudo-Random Generator (PRG). Therefore, the key remains random up to a negligible probability for any Probabilistic Polynomial Time (PPT) adversary. As the key is not perfectly random, a stream cipher relaxes the theoretical notion of perfect secrecy of the OTP, and it can only achieve computational security (see Unconditional vs. Conditional Security). This relaxation in security brings in a real advantage, in the sense that the keystream used for encryption can be derived from a shorter key k, the seed fed into the PRG. As the PRG is deterministic, if both parties know the seed k then they can derive the keystream and thus perform encryption and/or decryption. Note that the way the PRG functions is part of the definition of the stream cipher, so it is public under Kerckhoffs' principle (see Principles); the only secret remains the seed fed into the PRG, namely k. This makes stream ciphers feasible in practice, compared to the OTP, which asks to transport and preserve a key of the size of the plaintext. In conclusion, stream ciphers bring a tradeoff between security and usability, being a less secure but easier usable variant of the OTP. 

As for the OTP, the keystream must always change. Otherwise, the security of the stream cipher (regardless of its internals) is compromised. This is archived by using a mode of operation, which brings in randomization (non-determinism) and can be either synchronous or asynchronous. 

In the synchronized mode [1], the seed k and an Initialisation Vector IV are seeded into the PRG to output the keystream. The keystream is then used to encrypt the plaintext. No part of the keystream is reused. Let the plaintexts be m1, m2, m3, ... in this order, without loss of generality. Then the corresponding ciphertexts will be c1 = m1 XOR keystream1, c2 = m2 XOR keystream2, ... The keystream is thus "consumed" in order: once a part is used, it will not be used again. This mode is synchronized, in the sense that it requires that both the sender and the receiver know the exact order (and length) of the messages so that the encryption and the decryption are performed using the same part of the keystream. If this does not hold, correctness fails (a ciphertext is decrypted with the wrong part of the key, resulting in a wrong plaintext). Note that IV is not hidden (again, from Kerckhoffs' principle (see Principles), only k must be private); in fact, IV is part of the ciphertext. Without knowing the value of the IV, the receiver could not decrypt. As it requires state preservation, the synchronized mode is suitable for a single communication session.

In the unsynchronized mode [1], the seed k remains unchanged, but the Initialisation Vector IV changes for each plaintext. This eliminates the (sometimes strict assumption) of synchronization between the sender and the receiver, as now the ciphertexts can be decrypted directly, regardless of their reception order in time. Again, the values of the IVs need to be known, so IV is again part of the ciphertext. The difference is that in synchronized mode, a single IV appends for multiple messages, while in unsynchronized mode, an IV appends for each message. More precise, Alice encrypts m1 and m2 into (IV1,c1) and (IV2,c2), with IV1 and IV2 distinct. The advantage of not requiring synchronization is clear, but it comes to the cost of an increased ciphertext length.

Note that, to preserve security, the PRG must remain secure when IV is known. In other words, its security must rely only on the private seed k. In particular, this means that PRG(IV,k) is pseudo-random (for any PPT adversary). Even more, for two distinct and randomly chosen IV1 and IV2, PRG(IV1,k) and PRG(IV2,k) must be independent and indistinguishable.

In practice, there are many examples of stream ciphers. Some of these examples include RC4, which is used in Wired Equivalent Privacy (WEP), and A5/1, which is used in 2G/GSM security. These are both examples of old and insecure ciphers, which have been proven vulnerable and cannot satisfy today's needs [2]. Because stream ciphers are fast to encrypt/decrypt and work well on less powerful devices, they are a good candidate for mobile and wireless communication, or lightweight cryptography, in general. More uo-to-date examples include the stream ciphers family SNOW [3] and ZUC [4] used in more recent generations of mobile communications. Competitions were open to define new stream ciphers to be used at a large scale, such as, e.g., eSTREAM. Currently, some of the candidates in the NIST lightweight cryptography standardization process are stream-based. 

[1] Kats, J., Lindell, Y. Introduction to Modern Cryptography, CRC Press. More info: http://www.cs.umd.edu/~jkatz/imc.html

[2] Van Tilborg, H. C., & Jajodia, S. (Eds.). (2014). Encyclopedia of cryptography and security. Springer Science & Business Media. Available at: https://www.researchgate.net/profile/Krzysztof-Kryszczuk/publication/230674947_Springer_Encyclopedia_of_Cryptography_and_Security 

[3] Ekdahl, P., & Johansson, T. (2000, November). SNOW-a new stream cipher. In Proceedings of first open NESSIE workshop, KU-Leuven (pp. 167-168).

[4] 3GPP. Universal Mobile Telecommunications System (UMTS); LTE; Specification of the 3GPP Confidentiality and Integrity Algorithms EEA3 & EIA3; Document 2: ZUC specification (3GPP TS 35.222 version 18.0.0 Release 18). Available at: https://www.etsi.org/deliver/etsi_ts/135200_135299/135222/18.00.00_60/ts_135222v180000p.pdf